Home

Although the study of cognition has been going on for over two thousand years, cognitive science as a recognized academic subject is relatively new. In the 1970s, it developed from converging research approaches in different subjects, namely neuroscience, anthropology, psychology, linguistics, artificial intelligence research (as part of computer science) and philosophy. Despite its interdisciplinary heritage, cognitive science is still largely characterized by a separation into various camps of computational modeling, neuroscience and cognitive science in the narrow sense (i.e. linguistics and psychology).

We are convinced that it is time to assemble the pieces of the puzzle of brain computation and to better integrate these separate disciplines. In order to gain a mechanistic understanding of how cognition is implemented in the brain, we follow the approach to build biologically plausible computational models that can perform cognitive tasks, and test such models with brain and behavioral experiments. A case in point is natural language understanding: based on linguistic theories of grammar, hypotheses of human language processing are tested by means of experiments. Furthermore, simulation models based on results obtained by neuroscience and artificial intelligence are developed, which in turn may lead to modified theories of grammar.

Analysis of continuous neuronal activity evoked by natural speech with computational corpus linguistics methods

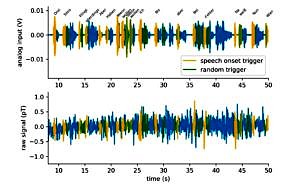
In the field of neurobiology of language, neuroimaging studies are generally based on stimulation paradigms consisting of at least two different conditions. Designing those paradigms can be very time-consuming and this traditional approach is necessarily data-limited. In contrast, in computational and corpus linguistics, analyses are often based on large text corpora, which allow a vast variety of hypotheses to be tested by repeatedly re-evaluating the data set. Furthermore, text corpora also allow exploratory data analysis in order to generate new hypotheses. By drawing on the advantages of both fields, neuroimaging and computational corpus linguistics, we here present a unified approach combining continuous natural speech and MEG to generate a corpus of speech-evoked neuronal activity.

Separability of data classes follows a master curve in the hidden layers of deep neural networks

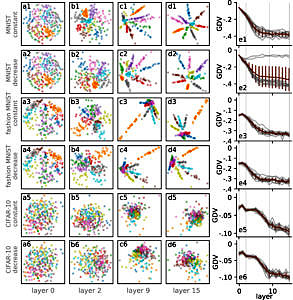Deep neural networks typically outperform more traditional machine learning models in their ability to classify complex data, and yet it is not clear how the individual hidden layers of a deep network contribute to the overall classification performance. We thus introduce a Generalized Discrimination Value (GDV) that measures, in a non-invasive manner, how well different data classes separate in each given network layer. The GDV can be used for the automatic tuning of hyper-parameters, such as the width profile and the total depth of a network. Moreover, the layer-dependent GDV(L) provides new insights into the data transformations that self-organize during training: In the case of multi-layer perceptrons trained with error backpropagation, we find that classification of highly complex data sets requires a temporal reduction of class separability, marked by a characteristic ‘energy barrier’ in the initial part of the GDV(L) curve. Even more surprisingly, for a given data set, the GDV(L) is running through a fixed ‘master curve’, independently from the total number of network layers. Furthermore, applying the GDV to Deep Belief Networks reveals that also unsupervised training with the Contrastive Divergence method can systematically increase class separability over tens of layers, even though the system does not ‘know’ the desired class labels. These results indicate that the GDV may become a useful tool to open the black box of deep learning.

“Recurrence Resonance” in three-neuron motifs

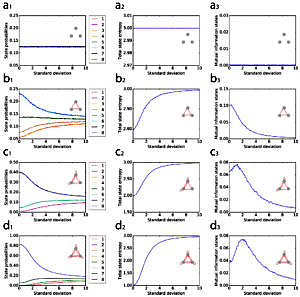Stochastic Resonance (SR) and Coherence Resonance (CR) are non-linear phenomena, in which an optimal amount of noise maximizes an objective function, such as the sensitivity for weak signals in SR, or the coherence of stochastic oscillations in CR. Here, we demonstrate a related phenomenon, which we call “Recurrence Resonance” (RR): noise can also improve the information flux in recurrent neural networks. In particular, we show for the case of three-neuron motifs with ternary connection strengths that the mutual information between successive network states can be maximized by adding a suitable amount of noise to the neuron inputs. This striking result suggests that noise in the brain may not be a problem that needs to be suppressed, but indeed a resource that is dynamically regulated in order to optimize information processing.

Weight statistics controls dynamics in recurrent neural networks

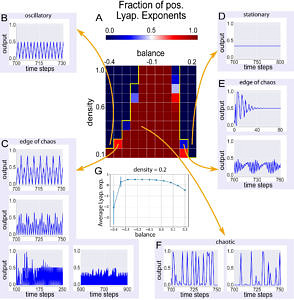Recurrent neural networks are complex non-linear systems, capable of ongoing activity in the absence of driving inputs. The dynamical properties of these systems, in particular their long-time attractor states, are determined on the microscopic level by the connection strengths wij between the individual neurons. However, little is known to which extent network dynamics is tunable on a more coarse-grained level by the statistical features of the weight matrix. In this work, we investigate the dynamics of recurrent networks of Boltzmann neurons. In particular we study the impact of three statistical parameters: density (the fraction of non-zero connections), balance (the ratio of excitatory to inhibitory connections), and symmetry (the fraction of neuron pairs with w_ij = w_ji). By computing a ‘phase diagram’ of network dynamics, we find that balance is the essential control parameter: Its gradual increase from negative to positive values drives the system from oscillatory behavior into a chaotic regime, and eventually into stationary fixed points. Only directly at the border of the chaotic regime do the neural networks display rich but regular dynamics, thus enabling actual information processing. These results suggest that the brain, too, is fine-tuned to the ‘edge of chaos’ by assuring a proper balance between excitatory and inhibitory neural connections.

Analysis of structure and dynamics in three-neuron motifs

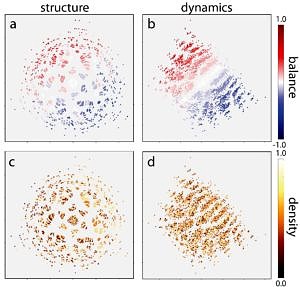Recurrent neural networks can produce ongoing state-to-state transitions without any driving inputs, and the dynamical properties of these transitions are determined by the neuronal connection strengths. Due to non-linearity, it is not clear how strongly the system dynamics is affected by discrete local changes in the connection structure, such as the removal, addition, or sign-switching of individual connections. Moreover, there are no suitable metrics to quantify structural and dynamical differences between two given networks with arbitrarily indexed neurons. In this work, we present such permutation-invariant metrics and apply them to motifs of three binary neurons with discrete ternary connection strengths, an important class of building blocks in biological networks. Using multidimensional scaling, we then study the similarity relations between all 3,411 topologically distinct motifs with regard to structure and dynamics, revealing a strong clustering and various symmetries. As expected, the structural and dynamical distance between pairs of motifs show a significant positive correlation. Strikingly, however, the key parameter controlling motif dynamics turns out to be the ratio of excitatory to inhibitory connections.